ADI_cond_neumann

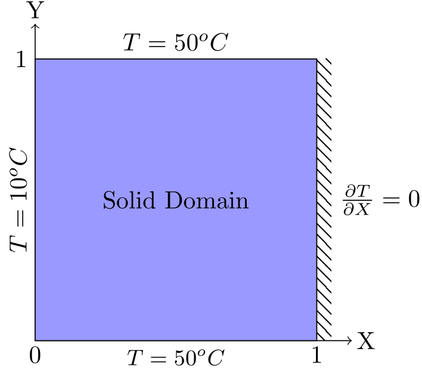
%ADI method with the implementation of TDMA is used to solve a 2D heat
%conduction with Neumann B.C at the right side (0<y<1 at x=1; du/dx=0)
%Dirichlet B.C. at left(0<y<1 at x=0; u=10), Top(0<x<1 at y=1; u=50) and Bottom(0<x<1 at y=0; u=50)
%Author Md Rysul Kabir
%Date 4/29/18

EQUATION TO BE SOLVED FOR THE PROBLEM:

Steady State Diffusion Equation, 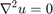${\nabla ^2u=0}$

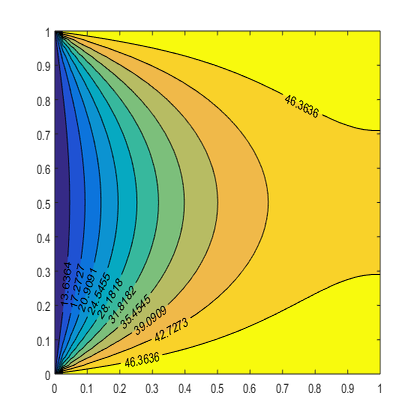
function m = ADI_cond_neumann
mx=40; my=40;
nx=mx+1; ny=my+1;
lx=1; ly=1;
x=linspace(0,lx,nx); y=linspace(0,ly,ny);
u=zeros(nx,ny);
u(1:nx,1:ny)=30;
u(1:nx,1)=50; u(1:nx,ny)=50; u(1,1:ny)=10; %u(nx,1:ny)=10; %B.C
uiter=u; unew_iter=u; errtol=1e-6;
error=2*errtol; iter=0; itermax=2000;
while ((error>errtol)&&(iter<itermax))
    %Horizontal sweep
    a(1:nx)=1;
    b(1:nx)=-4;
    c(1:nx)=1;
    d(1:nx)=0;
    for j=2:ny-1
        for i=2:nx-1
            d(i)=-(uiter(i,j-1)+uiter(i,j+1));
        end
        a(1)=0; b(1)=1; c(1)=0;%Dirichlet B.C
        a(nx)=-1; b(nx)=1; c(nx)=0;%Neumann B.C
        d(1)=u(1,j); %Dirichlet b.c
        d(nx)=0; %Neumann b.c
        unew_iter(1:nx,j)=solver_tdma(nx,a,b,c,d);
    end
    uiter=unew_iter;
    %Vertical sweep
    for i=2:nx-1
        a(1:ny)=1;
        b(1:ny)=-4;
        c(1:ny)=1;
        d(1:ny)=0;
        for j=2:ny-1
            d(j)=-(uiter(i-1,j)+uiter(i+1,j));
        end
        a(1)=0; b(1)=1; c(1)=0;%Dirichlet B.C
        a(ny)=0; b(ny)=1; c(ny)=0;%Dirichlet B.C
        d(1)=u(i,1); %required for dirichlet b.c
        d(ny)=u(i,ny); %required for dirichlet b.c
        unew_iter(i,1:ny)=solver_tdma(ny,a,b,c,d);
    end
    error=sum(sum(abs(unew_iter-uiter)))/sum(sum(abs(unew_iter)));
    uiter=unew_iter;
    iter=iter+1; %To count the number of iteration for a certain initial value
end
m=uiter';
[C,H]=contourf(x,y,m,10,'k-');colormap;
clabel(C,H,'LabelSpacing',500);
end